|
Electric Guitar Necks: What's the difference?
Electric guitar necks, or for this exercise stratocaster electric guitar necks, and stratocaster clone necks, look very much the same. Other than the type of wood used for the fingerboard, it's hard to tell what to look for, or what to choose. Here's what we're going to look at: 
---Neck Radius ---Types of Wood ---The Headstock ---Fret Size ---Number of Frets ---Truss Rod Adjustment location 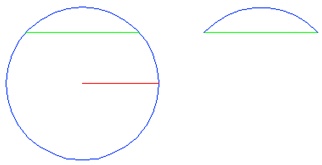
The Neck radius for some reason, seems to be one of the more confusing issues I find out there on the Web. So using my hokey sketch here I'll attempt to demystify what the neck radius is. The fingerboard of the neck is curved from side to side. The amount of curvature is described in terms of a radius. Now of course there are no circles involved with an electric guitar neck, but the curved fingerboard represents a piece of a circle. My sketch shows a full circle in blue, with the radius marked in red. The green line cuts the circle so we are left with an arc, which sort of looks like the profile of a guitar neck. What the radius describes is how flat the fingerboard is, a larger radius always results in a flatter fingerboard. Conversely a smaller radius always results in a more curved fingerboard. Which one you choose is a matter of preference. For the string bending maniac, usually a larger radius is preferred because the flatter neck doesn't fret out, giving you more room to bend. For the chord player a more curved surface is usually preferred, so you don't have to stretch your fingers so far. There are compound radius necks that try and serve both purposes. Again, the choice is always up to you, and how you play. The type of wood primarily used to build electric guitar necks, or I should say electric guitar necks in the Fender variety, is Maple. You'll find a lot of mahogany on acoustics, and Gibsons. Maple is a nice, hard, clear, abundant wood that works well as neck material. There are different varieties of maple like the stock used to make the Birdseye maple neck shown above. Fingerboards are most commonly made of maple, or Brazilian rosewood. There used to be a wider range of fingerboard material, but many of it has been banned for use. This is one of the many reasons vintage guitars can have so much value. There is much talk about the brightness of maple versus rosewood, now I'm no virtuoso, but we're talking electric guitars here. If you want more brightness turn up the treble, or adjust the tone. I do find that I can play a wee bit faster on a slick maple neck though.

In the beginning of my guitar obsession I thought all stratocaster electric guitar necks were the same shape. Then I found the 70's era strat neck, and realized the headstock was bigger than other strat headstocks. This I found to be purely cosmetic. Everything else is the same, like the location of the tuner holes and the nut. Another thing you may have noticed is the mahogany strip, or "skunk stripe" running the length of the neck back. This is part of the manufacturing process, and provides a groove to lay the truss rod in. However, like the neck shown at the top of the picture above, there are necks with no skunk stripe. And this neck does have a truss rod. Again, I believe this is cosmetic, and has no real bearing on the function of the neck. 

Another thing to consider is the size of the fret wire. I'm not certain of how many different sizes there are, and can't seem to find a definitive answer, but I have measured five different sizes from small to jumbo. I've also been looking for an answer as to what each size is good for and that seems to be aloof as well. What I can tell you is that the height of the fret from the fingerboard, seems to stay consistent, regardless of the width. Physics tells me that a wider fret will last longer due to it's decrease in radius, and resulting larger contact patch. Having played with both narrow, and jumbo, it does seem easier to do neck slides, though not enough easier to make me want to change every neck with jumbo frets. I think the fret size is much like most other things concerning the guitar, it's subjective to taste, and what you're used to. I do think that heavy handed players, like myself will benefit from larger frets because they'll wear slower. Light handed players may benefit from smaller frets, because the smaller contact patch allows the string to sound easier. 
The last thing I'm going to touch on is the location of the truss rod adjustment. Fortunately the truss rod is something you may never need to get at. At most you might need a tweak every year, or couple of years. Nowadays the most common location for the adjustment is out at the headstock. But you can still find guitar necks, and I just built a guitar using one, that has the adjustment at the heal of the guitar neck. This isn't the end of the world, it just means the neck must come off the body in order to adjust the truss rod. Personally I like the look of the neck with no truss rod adjustment hole, but the convenience is without question, and is probably why most necks have the adjustment out at the headstock. Oh, I almost forgot, you can get electric guitar necks commonly with 21 or 22 frets, the difference is shown above in the side view of the two neck heels. Note that the neck with the rosewood fingerboard hangs over the edge. This is a 22 fret neck, the maple neck that has a flush fingerboard has 21 frets. I typically go for the 22 frets because it hangs out over the pickguard, and covers up an otherwise exposed seam. However the 21 fret neck allows easier removal of the pickguard. I certainly don't play on the 21st fret, maybe if your into tapping this is important. As always I hope this helps more than confuses, your comments are always welcome, peace JB.
Return from Electric Guitar Necks to Electric Guitar Info home |




